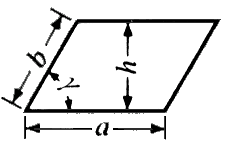
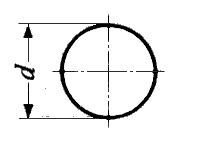
** 도형의 면적 계산식 예시 업무상 가끔은 사용하게 되는 면적계산과 관련된 기본 공식들을 소개합니다. 아래에서 사용하는 기호는 다음과 같습니다. 삼각형 A = a x h / 2 사각형 A = a x h 사다리꼴 A = (a + b) x h / 2 평행사변형 A = a x h = a x b x Ain 원 A = π x = π x 고리 A = π x ( = π x ( 부채꼴 A = π x = 0.00873 x ( 원호 A = ≒ 선분 호의 높이 육각형 A = ≒ 0.866 x e = 2 x 타원형 A = π x ≒ 0.785 x U ≒ 0.75 x π x ( ** 도형의 체적 계산식 예시 아래에서 사용하는 기호는 다음과 같습니다. 원기둥(환봉) V = π x M = π x S = π x 사각뿔 V = a x h / 3 원뿔 V = π x M = π x S = π x 원뿔대 V = π x h x ( M = π x ( S = 구 V = π x S = π x 구 조각 V = π x M = 2 x π x 부채꼴 구 V = 2π x S = π x 평행으로 잘린 구 V = π x M = 2 x π x 링 V = S = 육각기둥 V = S = ( ≒ 1.732 x 표면적(S) 과 대변길이(s)를 잘 구분하세요. 중공축 V = π x ( = π x ( ☞ 위 식에서 구해진 체적(V)에 비중을 곱하면 무게가 됩니다. 참고로 대표적 물질의 비중값은 아래와 같습니다. 재질명 비중 재질명 비중 알루미늄 2.7 g/㎤ 강 7.9 g/㎤ 동 8.93 g/㎤ 고무 1.08 g/㎤
A : 면적 (Area)
a : 밑변길이
h : 높이 (height)
d : 지름 (diameter)
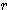 : 반경 (radius)
: 반경 (radius)
U : 원둘레
π : 원주율 (= 3.14159 )
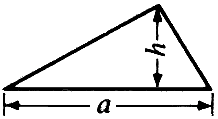
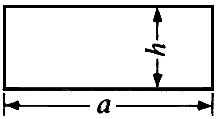
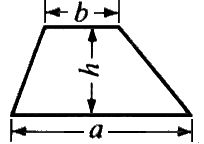
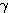
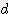 x
x 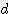 / 4
/ 4 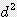 / 4 ≒ 0.785
/ 4 ≒ 0.785 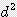
U = π x 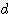
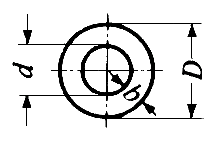
 ) / 4
) / 4 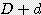 ) x
) x 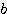 / 2
/ 2
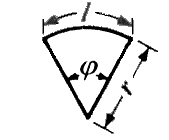
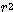 x
x 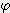 / 360
/ 360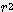 x
x 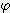
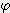 = 각도(degree), π = 3.14159 )
= 각도(degree), π = 3.14159 )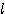 = π x
= π x  x
x 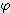 / 180 = 0.0175 x
/ 180 = 0.0175 x 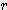 x
x 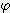

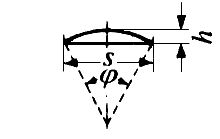
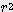 (π x
(π x 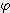 / 180 - sin
/ 180 - sin 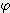 ) / 2
) / 2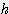 x
x 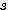 x [ 0.667 +
x [ 0.667 + 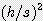 ]
]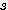 = 2 x
= 2 x 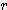 x sin (
x sin ( 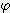 / 2 )
/ 2 )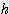 =
= 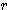 x ( 1 - cos (
x ( 1 - cos ( 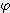 / 2 ))
/ 2 ))

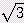 x
x 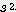 / 2
/ 2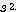
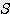 /
/ 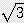 ≒ 1.155
≒ 1.155 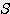
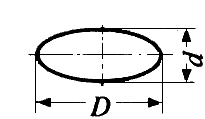
 x
x 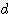 / 4
/ 4 x
x 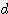
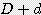 ) - 0.5 x π x
) - 0.5 x π x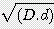
업무상 가끔은 사용하게 되는 체적계산과 관련된 기본 공식들을 소개합니다.
V : 체적 (Volume)
M : 측면적 (상하 단면을 제외한 측면의 표면적을 의미, lateral area)
S : 표면적 (상하 단면을 포함한 전체 표면적, Surface area)
A : 면적 (Area)
a : 밑변길이
h : 높이 (height)
d : 지름 (diameter)
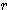 : 반경 (radius)
: 반경 (radius)
U : 원둘레
π : 원주율 (= 3.14159 )
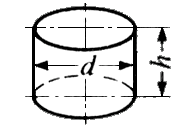
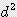 x h ≒ 0.785
x h ≒ 0.785 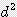 x h
x h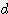 x h
x h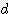 x (
x ( 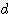 /2 + h)
/2 + h)
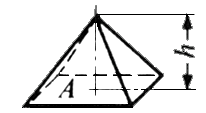
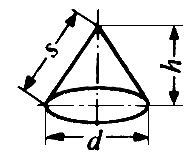
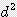 x h / 12 ≒ 0.262
x h / 12 ≒ 0.262 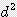 x h
x h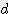 x s / 2 = 0.785
x s / 2 = 0.785 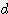 x
x 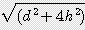
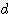 x (
x ( 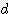 /2 + s) / 2
/2 + s) / 2
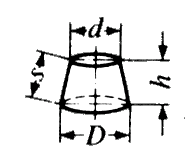
 +
+  x
x 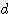 +
+ 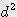 ) / 12
) / 12
≒ 0.262 x h x ( +
+  x
x 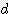 +
+ 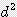 )
) +
+ 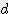 ) x s / 2
) x s / 2 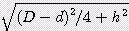

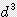 / 6 ≒ 0.524
/ 6 ≒ 0.524 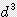
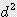
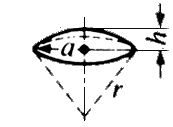
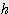 x (3 x
x (3 x  ) / 6
) / 6
= π x 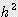 x (3 x
x (3 x 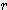 -
- 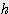 ) / 3
) / 3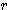 x
x 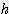 = π x (
= π x (  )
)
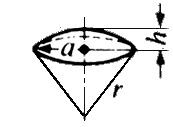
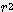 x
x 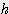 / 3
/ 3
= 2.094 x 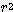 x
x 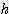
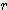 x (2
x (2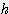 +
+ 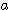 )
)
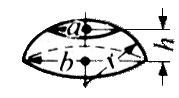
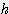 (
(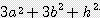 ) / 6
) / 6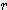 x
x 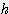
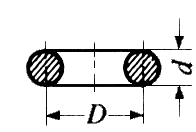
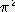 x
x  x
x 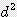 / 4 = 2.467 x
/ 4 = 2.467 x  x
x 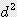
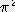 x
x  x
x 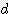 = 9.870 x
= 9.870 x  x
x 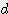
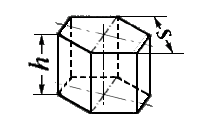
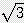 x
x 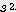 x
x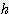 / 2
/ 2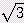 x
x 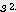 / 2) x 2 + 6 x s x
/ 2) x 2 + 6 x s x 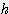 /
/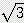
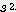 + 10.392 x s x
+ 10.392 x s x 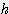
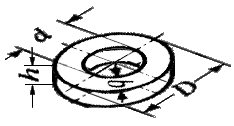
 ) x
) x 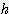 / 4
/ 4 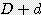 ) x
) x 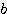 x
x 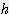 / 2
/ 2
'기술 정보' 카테고리의 다른 글
| [스크랩] 일본용접협회에서 퍼온 동영상(CO2용접) (0) | 2009.08.11 |
|---|---|
| [스크랩] 일본 용접협회서 퍼온 동영상(CO2수평, 파이프) (0) | 2009.08.11 |
| [스크랩] 용접부에 발생하는 결함 용어 (0) | 2009.07.19 |
| 압력용기 강재 생산기술 (0) | 2009.01.10 |
| [스크랩] 압력용기 두께 (0) | 2009.01.10 |